A
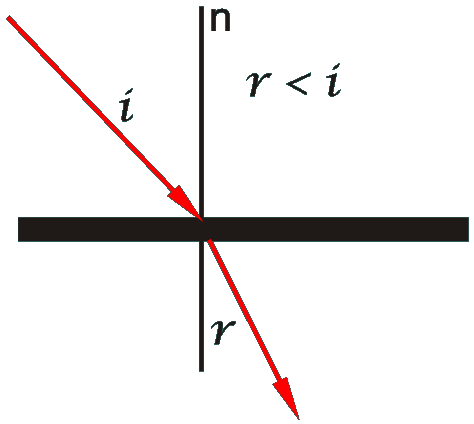
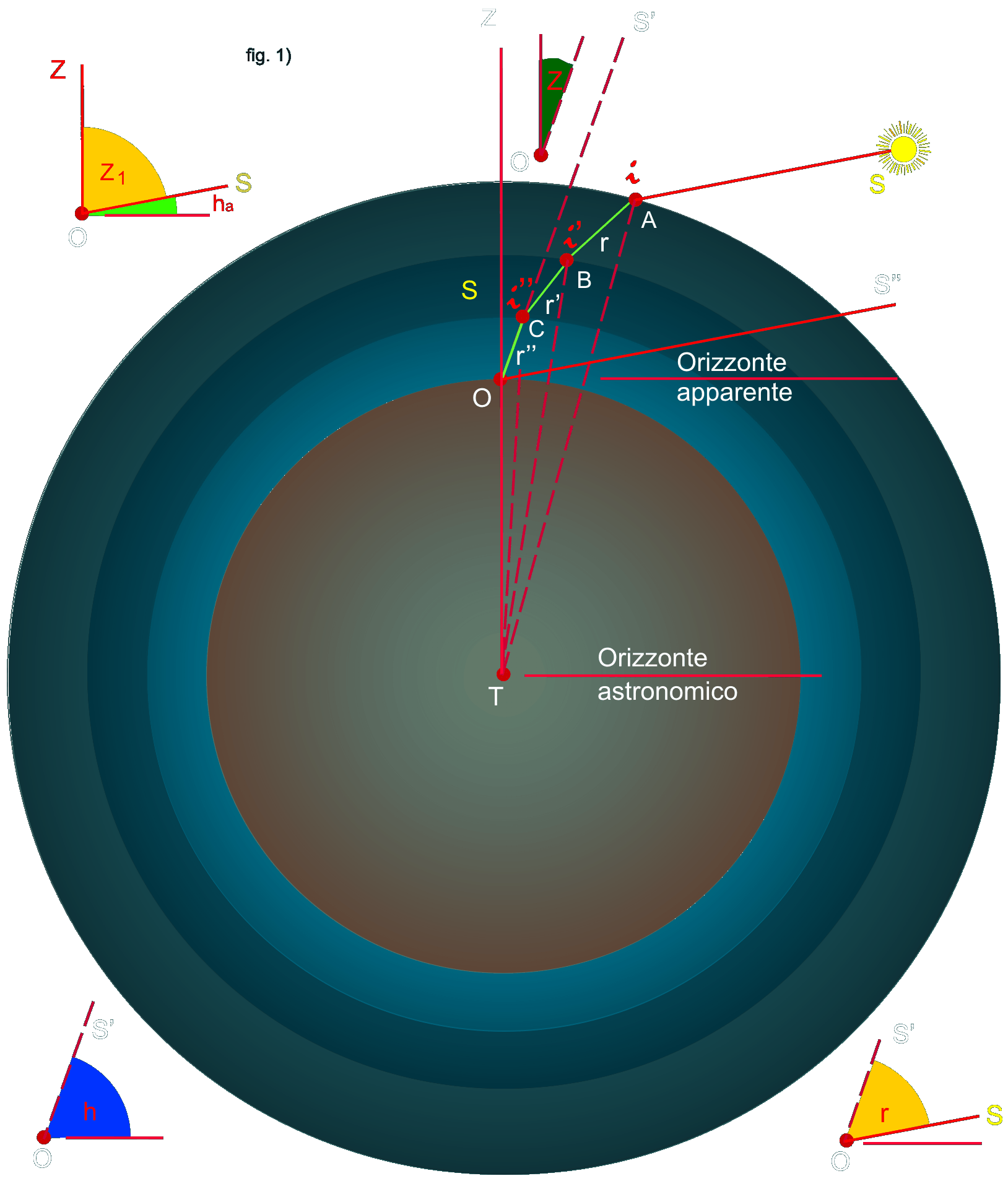
causa del susseguirsi dei diversi strati atmosferici, la rifrazione
astronomica è raffigurata attraverso la spezzata SABCO, l’osservatore vede il raggio
S
innalzato secondo la direzione S’. Se gli strati atmosferici sono
numerosi e infinitamente sottili la spezzata ASBCO può essere
interpretata come una curva con concavità rivolta verso la terra.
n = coef. rifrazione
dell'aria funzione (T,P,r)
A titolo indicativo, di
seguito vengono illustrati alcuni valori dell'indice di rifrazione n
| Mezzo
o Sostanza |
Indice di Rifrazione
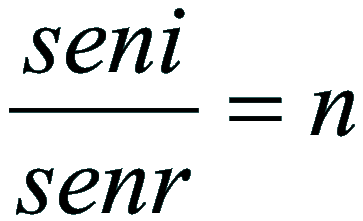 |
| Vuoto |
1 |
| Aria (C°=0; p=1013,25hp) |
1,000297 |
| Acqua (23°) |
1,33 |
| Ghiaccio |
1,31 |
| Vetro |
1,65 |
| Diamante |
2,417 |
| Quarzo |
1,51 |
Calcolo Della
Rifrazione Astronomica ( r'' )
Individuato
con r'' l'angolo del raggio rifratto dall'ultimo strato
atmosferico
in prossimità del suolo dove è posto l'osservatore e ponendo:
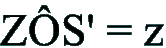

 = =  fig.1) fig.1)
sostituendo:
1)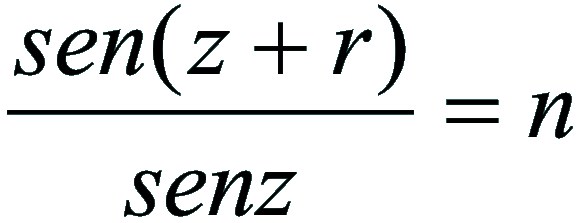
Ma essendo la distanza zenitale il complemento dell'altezza, risulta:
l

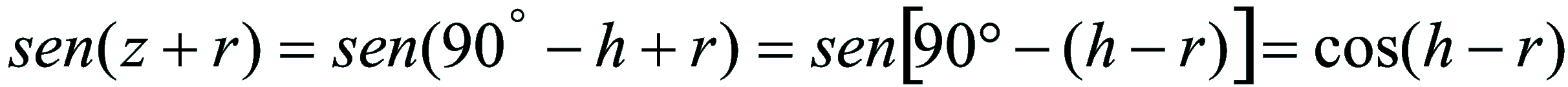
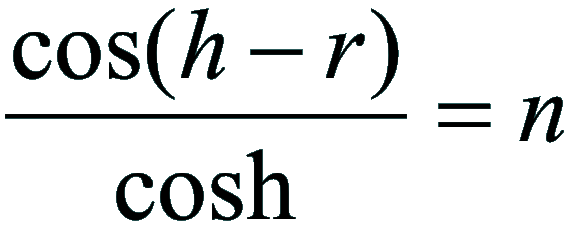
sviluppando il coseno:
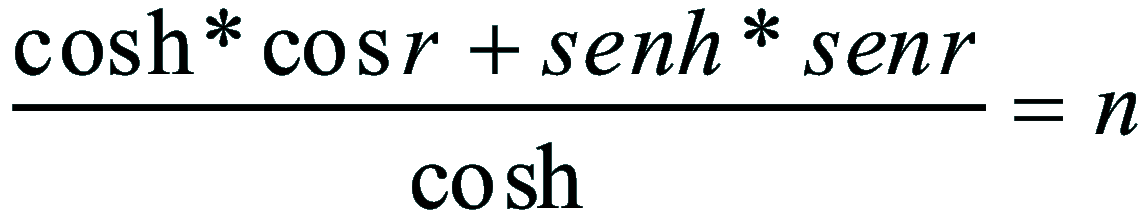
ed eseguendo la divisione:
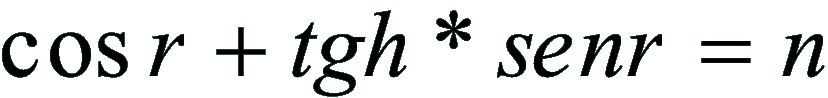
Poichè la rifrazione astronomica è molto piccola si può porre:*
2)
3)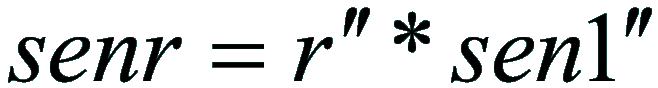
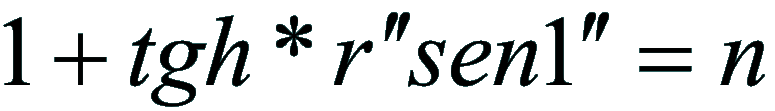
4)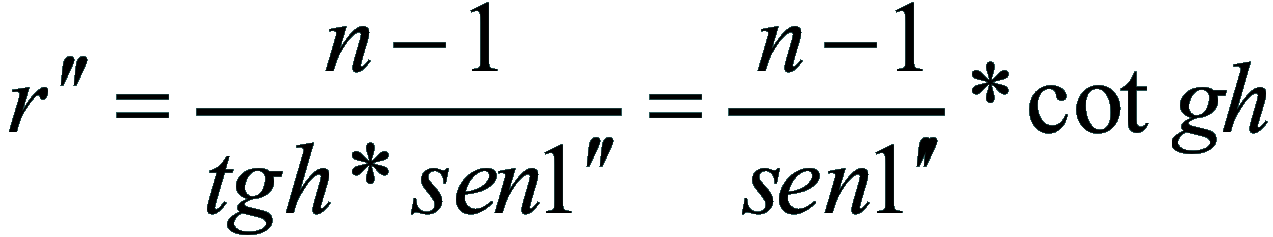
ma pochè n=1,000297
sostituendo tale valore nella formula 4)
5)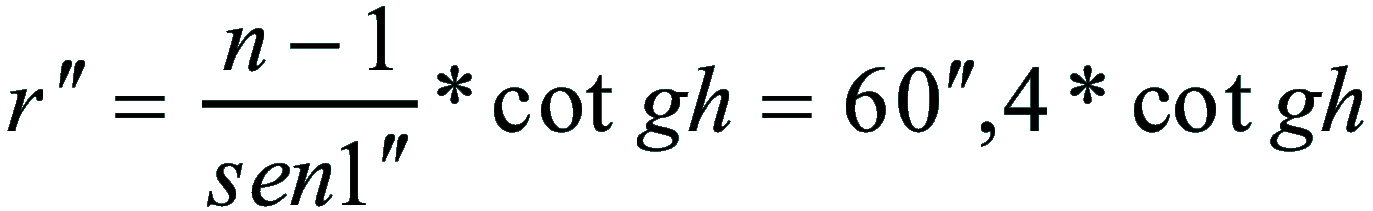
|
|
 |
The Explanatory Supplement to the Astronomical
Almanac
Come
si può arguire l'entità della rifrazione dipenderà dalla densità
dell'aria, dipendente a sua volta dalla temperatura e dalla pressione.
Delle
formule rigorose per quantificare la rifrazione sono piuttosto
complesse. Una versione che pur beneficiando di alcune approssimazioni
è capace di dare una quantificazione abbastanza buona è data dalle due
seguenti formule (da "The Explanatory Supplement to the Astronomical
Almanac")**
per Z < 75°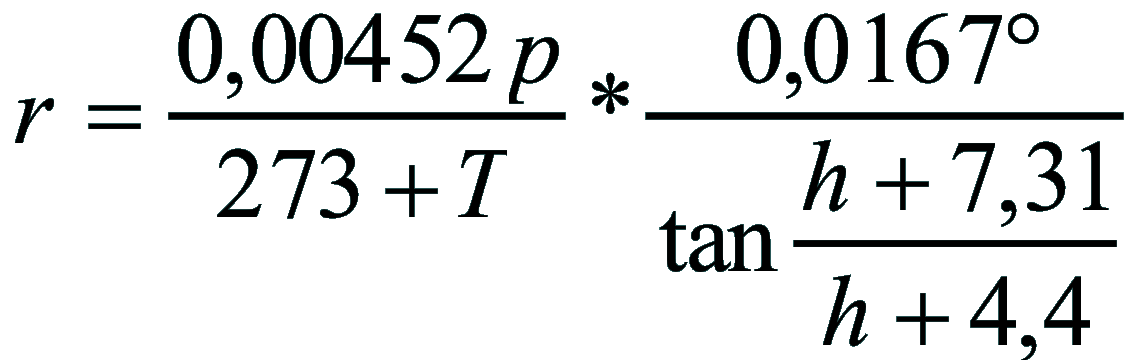
per Z > 75°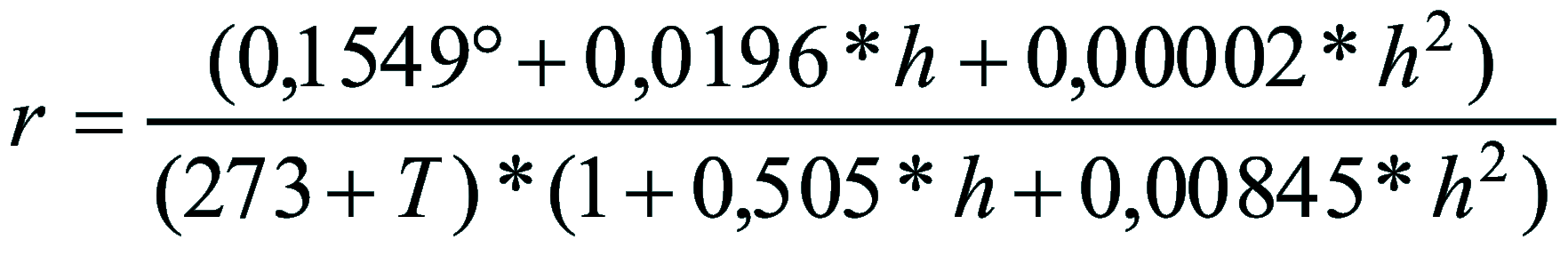
dove
r è la rifrazione espressa in gradi, P è la pressione, espressa
in hPa o mbar, T è la temperatura, espressa in °C, h è l'altezza
dell'astro espressa in gradi sessagesimali. Sono date due formule, una con distanza zenitale (z) minore di 75° ed un'altra con
distanza
zenitale maggiore perché nel secondo caso si fa l'approssimazione di
atmosfera a strati piani paralleli che per z<75° non è più
consistente.
In condizioni di pressione e temperatura standard,
per un oggetto posto sull'orizzonte (h=0°) la rifrazione è dell'ordine
dei 30'.
Se abbiamo sia il Sole che la Luna molto bassi
sull'orizzonte entrambi possono essere affetti da 30' di rifrazione,
per un totale di 1°.
Esistono
molte tavole che permettono di ottenere l'importo della rifrazione
astronomica r'' in funzione di z (o di h), calcolato per uno specifico
valore di temperatura e di pressione al suolo, fornendo anche le dovute
correzioni per i veri valori di questi due fondamentali parametri
fisici dell'atmosfera. Nella raccolta delle Tavole Nautiche
dell'Istituto
Idrografico della Marina viene dato il valore di r calcolato per temperatura e pressione al suolo di t=10°C e p=760
mm con la possibilità di correggerlo sia per temperature che
per
pressioni differenti dai valori standard considerati, attraverso interpolazione lineare.
| Osservazione
In coincidenza dei giorni del 21 Marzo e 23 Settembre l'osservatore è posto sul piano equinoziale e vede il sole muoversi velocemente in cielo dal sorgere al tramonto. In questa circostanza, poiché lo spessore dello strato atmosferico attraversato dai raggi luminosi risulta essere minimo "numero degli strati omogenei basso", la componente diretta della radiazione solare risulta essere massima e la luce solare tende ad assumere una colorazione bianca. Inoltre, la diminuzione dello spessore dello strato atmosferico attraversato dai raggi solari comporta la riduzione del fenomeno rifrattivo, che alle alte latitudini risulta essere sensibilmente maggiore rispetto alle medie e basse latitudini. Per chiarire meglio questo concetto immaginiamo di tagliare il bulbo di una cipolla con due piani di sezione in direzione ortogonale alla Gemma. Si osserva che gli spessori di cerchi concentrici dei catafilli sono maggiori in prossimità del taglio in vicinanza alla Gemma. Al contrario, i giorni solstiziali del 21 Giugno e 22 Dicembre l'osservatore non è posto sui piani solstiziali e vede il sole muoversi lentamente in cielo dal sorgere al tramonto. In questa circostanza, poiché lo spessore dello strato atmosferico attraversato dai raggi luminosi risulta essere maggiore "numero degli strati omogenei alto", il fenomeno rifrattivo è più accentuato rispetto all'equinozio e il sole appare giallo per l'alterarsi delle lunghezze d'onda nel range dello spettro della luce solare visibile.
| * Ferdinando Flora,
| Astronomia Nautica (Navigazione Astronomica) pag. 101, Hoepli, 1987
Milano. | | ** P. Kenneth Seidelmann, | United States Naval Observatory. Nautical Almanac Office
pag.144 |
|
|